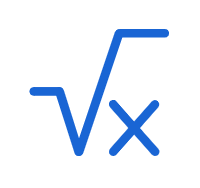Si buscas responder a la siguiente pregunta: “¿cuál es la raíz cuadrada de 43?” la respuesta es 6.557438524302
RESPUESTA: raíz cuadrada de 43=6.557438524302
La raíz cuadrada de un número (43 en este caso) es un número (6.557438524302 en este caso) que multiplicado por sí mismo es igual al número del que estás calculando la raíz cuadrada (43). La raíz cuadrada de 43 se puede expresar en forma radical o exponencial como se muestra a continuación:
- Forma radical de la raíz cuadrada de 43: √43
- Forma exponencial de la raíz cuadrada de 43: (43)½ o (43)0.5
Este símbolo √ se llama signo radical o base. El número cuya raíz cuadrada se calcula se llama radicando. El radicando es el número debajo del signo radical (base), en este caso es 43.
Calculadora de raiz cuadrada de 43
Si desea confirmar la respuesta a la pregunta “¿cuál es la raíz cuadrada de 43?” o calcule una raíz cuadrada de cualquier otro número use la calculadora de raíz cuadrada:
Guía de cálculo de la raíz cuadrada de 43
En las siguientes secciones explicamos cómo calcular la raíz cuadrada de 43. Responderemos preguntas tan comunes como: “¿la raíz cuadrada de 43 es racional o irracional?” y “¿43 es un cuadrado perfecto?” Discutiremos cuál es la raíz cuadrada principal de 43. Para su referencia, también incluimos las siguientes tablas:
- Raíces enésimas de 43
- Números cuadrados perfectos
- Raíces cuadradas de números alrededor de 43
Encontrará toda la información que necesita sobre los cálculos de la raíz cuadrada de 43 a continuación.
¿Cuál es la raíz cuadrada de 43?
La raíz cuadrada de 43 es un número que multiplicado por sí mismo da 43. Por tanto, la raíz cuadrada de 43 es 6.557438524302 y lo escribimos √43=6.557438524302 porque 6.5574385243022=43. Como 6.5574385243022 es lo mismo que 6.557438524302 x 6.557438524302, las siguientes expresiones son verdaderas:
43 = 6.5574385243022=6.557438524302×6.557438524302
Por lo tanto
RESPUESTA: raíz cuadrada de 43=√43=6.557438524302
¿43 es un cuadrado perfecto?
Un número se considera un cuadrado perfecto si es producto de elevar al cuadrado un número entero (llamado entero). 0, 1, 2, 3, 4, 7, 8 y 9 son todos números enteros (igual que los números enteros). Números como -8, 7.025 o 5 ½ no son números enteros. Recuerda que elevar al cuadrado es cuando un número se multiplica por sí mismo. Por ejemplo, 81 es un cuadrado perfecto porque es un producto de 92 que es lo mismo que 9×9. El aviso 9 es un número entero (entero).
En nuestro ejemplo, la raíz cuadrada de 43 es 6.557438524302. Dado que 6.557438524302 no es un numero entero, entonces 43 no es un cuadrado perfecto.
RESPUESTA: 43 no es un numero entero
¿La raíz cuadrada de 43 es un número racional o irracional?
Un número es racional cuando se puede formar dividiendo un número entero por otro número entero. Un número entero no tiene una parte fraccionaria. Simplemente dijo que un número es racional si se puede escribir como una fracción.
Un método rápido para determinar si 43 es un cuadrado perfecto. Las raíces cuadradas de cuadrados perfectos son todos números racionales. Las raíces cuadradas de números que no son un cuadrado perfecto son todos números irracionales. Como sabemos que 43 no es un cuadrado perfecto por lo tanto 43 no es un numero racional.
Raíz cuadrada principal de 43
Todo número positivo tiene dos raíces cuadradas. Una de las raíces cuadradas es positiva y la otra es negativa. Por ejemplo, las raíces cuadradas de 43 son -6.557438524302 (negativo) y +6.557438524302 (positivo) porque (-6.557438524302)^2=(+6.557438524302)^2=43. La raíz cuadrada positiva se llama raíz cuadrada principal. Por lo general, cuando calculamos “la raíz cuadrada de un número”, nos referimos a la raíz cuadrada principal. En nuestro caso, es 6.557438524302 positivo o +6.557438524302, que se escribe como 6.557438524302. Como sabrá, si no hay un signo menos (-) antes de un número, es un número positivo.
La raíz cuadrada principal de 43 es 6.557438524302.
Calcular la raíz cuadrada de 43 con una calculadora
Para calcular la raíz cuadrada de 43 con una calculadora básica o científica, debe ingresar 43 y luego presionar la tecla con este signo “√x”
√43 = 6.557438524302
Cálculo de la raíz cuadrada de 43 en Excel y Google Sheets
Hay dos funciones que puede usar para hacer este cálculo. Puede usar la función SQRT () para calcular la raíz cuadrada de cualquier número en Excel y Google Sheets. Haga clic en una celda y escriba =SQRT(43). Presione enter. Obtendrás 6.557438524302.
También puede usar la función POTENCIA que funciona como un exponente es una ecuación. Para encontrar una raíz cuadrada de 43 escriba =POTENCIA (43, 1/2). Recuerde que las raíces cuadradas se pueden expresar como exponentes como discutimos anteriormente en este artículo.
Tabla: Raíces enésimas de 43
En la sección anterior explicamos cómo se calcula la raíz cuadrada (que es la segunda raíz) de 43. Sin embargo, hay más raíces de 43. Encuentra las raíces enésimas de 43 en la siguiente tabla:
| Índice (N) | Raíz de Radicano | Expresión | Raíz |
| 2 | Raíz cuadrada de 43 | ²√43 | 6.557 |
| 3 | Raíz cúbica de 43 | ³√43 | 3.503 |
| 4 | Cuarta raíz de 43 | ⁴√43 | 2.561 |
| 5 | Quinta raíz de 43 | ⁵√43 | 2.122 |
| 6 | Sexta raíz de 43 | ⁶√43 | 1.872 |
| 7 | Séptima raíz 43 | ⁷√43 | 1.711 |
| 8 | Ocho Raíz de 43 | ⁸√43 | 1.600 |
| 9 | Novena raíz de 43 | ⁹√43 | 1.519 |
| 10 | Raíz décima de 43 | ¹⁰√43 | 1.519 |
Tabla: raíz cuadrada de números alrededor de 43
Esta tabla enumera números alrededor de 43 y sus respectivas raíces cuadradas.
| NÚMERO | RAÍZ CUADRADA |
| 38 | 6.164 |
| 39 | 6.245 |
| 40 | 6.325 |
| 41 | 6.403 |
| 42 | 6.481 |
| 43 | 6.557438524302 |
| 44 | 6.633 |
| 45 | 6.708 |
| 46 | 6.782 |
| 47 | 6.856 |
| 48 | 6.928 |
Tabla: Lista de números cuadrados perfectos
Esta tabla enumera números cuadrados perfectos del 1 al 10,000.
| Cuadrados perfectos | Raíz cuadrada | Número entero |
| 1 | √ 1 = | 1 |
| 4 | √ 4 = | 2 |
| 9 | √ 9 = | 3 |
| 16 | √ 16 = | 4 |
| 25 | √ 25 = | 5 |
| 36 | √ 36 = | 6 |
| 49 | √ 49 = | 7 |
| 64 | √ 64 = | 8 |
| 81 | √ 81 = | 9 |
| 100 | √ 100 = | 10 |
| 121 | √ 121 = | 11 |
| 144 | √ 144 = | 12 |
| 169 | √ 169 = | 13 |
| 196 | √ 196 = | 14 |
| 225 | √ 225 = | 15 |
| 256 | √ 256 = | 16 |
| 289 | √ 289 = | 17 |
| 324 | √ 324 = | 18 |
| 361 | √ 361 = | 19 |
| 400 | √ 400 = | 20 |
| 441 | √ 441 = | 21 |
| 484 | √ 484 = | 22 |
| 529 | √ 529 = | 23 |
| 576 | √ 576 = | 24 |
| 625 | √ 625 = | 25 |
| 676 | √ 676 = | 26 |
| 729 | √ 729 = | 27 |
| 784 | √ 784 = | 28 |
| 841 | √ 841 = | 29 |
| 900 | √ 900 = | 30 |
| 961 | √ 961 = | 31 |
| 1024 | √ 1024 = | 32 |
| 1089 | √ 1089 = | 33 |
| 1156 | √ 1156 = | 34 |
| 1225 | √ 1225 = | 35 |
| 1296 | √ 1296 = | 36 |
| 1369 | √ 1369 = | 37 |
| 1444 | √ 1444 = | 38 |
| 1521 | √ 1521 = | 39 |
| 1600 | √ 1600 = | 40 |
| 1681 | √ 1681 = | 41 |
| 1764 | √ 1764 = | 42 |
| 1849 | √ 1849 = | 43 |
| 1936 | √ 1936 = | 44 |
| 2025 | √ 2025 = | 45 |
| 2116 | √ 2116 = | 46 |
| 2209 | √ 2209 = | 47 |
| 2304 | √ 2304 = | 48 |
| 2401 | √ 2401 = | 49 |
| 2500 | √ 2500 = | 50 |
| 2601 | √ 2601 = | 51 |
| 2704 | √ 2704 = | 52 |
| 2809 | √ 2809 = | 53 |
| 2916 | √ 2916 = | 54 |
| 3025 | √ 3025 = | 55 |
| 3136 | √ 3136 = | 56 |
| 3249 | √ 3249 = | 57 |
| 3364 | √ 3364 = | 58 |
| 3481 | √ 3481 = | 59 |
| 3600 | √ 3600 = | 60 |
| 3721 | √ 3721 = | 61 |
| 3844 | √ 3844 = | 62 |
| 3969 | √ 3969 = | 63 |
| 4096 | √ 4096 = | 64 |
| 4225 | √ 4225 = | 65 |
| 4356 | √ 4356 = | 66 |
| 4489 | √ 4489 = | 67 |
| 4624 | √ 4624 = | 68 |
| 4761 | √ 4761 = | 69 |
| 4900 | √ 4900 = | 70 |
| 5041 | √ 5041 = | 71 |
| 5184 | √ 5184 = | 72 |
| 5329 | √ 5329 = | 73 |
| 5476 | √ 5476 = | 74 |
| 5625 | √ 5625 = | 75 |
| 5776 | √ 5776 = | 76 |
| 5929 | √ 5929 = | 77 |
| 6084 | √ 6084 = | 78 |
| 6241 | √ 6241 = | 79 |
| 6400 | √ 6400 = | 80 |
| 6561 | √ 6561 = | 81 |
| 6724 | √ 6724 = | 82 |
| 6889 | √ 6889 = | 83 |
| 7056 | √ 7056 = | 84 |
| 7225 | √ 7225 = | 85 |
| 7396 | √ 7396 = | 86 |
| 7569 | √ 7569 = | 87 |
| 7744 | √ 7744 = | 88 |
| 7921 | √ 7921 = | 89 |
| 8100 | √ 8100 = | 90 |
| 8281 | √ 8281 = | 91 |
| 8464 | √ 8464 = | 92 |
| 8649 | √ 8649 = | 93 |
| 8836 | √ 8836 = | 94 |
| 9025 | √ 9025 = | 95 |
| 9216 | √ 9216 = | 96 |
| 9409 | √ 9409 = | 97 |
| 9604 | √ 9604 = | 98 |
| 9801 | √ 9801 = | 99 |
| 10000 | √ 10000 = | 100 |
Visite raizcuadradade.com para cualquier cálculo relacionado con raíces cuadradas, incluidas raíces cuadradas, raíces cuadradas negativas, raíces cuadradas de fracciones, exponenciación y otros cálculos relacionados.